A few weeks ago, when news broke of PSA’s purchase of Genamint, we briefly discussed the card grading market and the importance of the “crack” - i.e., the difference in price between a graded card and a raw card.
In that article, we noted that PSA-graded cards tended to have the highest crack and that that is very good for business over at PSA. But what causes graded cards to be more valuable than raw cards and, more importantly, how much more valuable should they be?
Like in previous articles, here we are concerned with value, not price. We know how much more expensive graded cards are - we can look at prices on eBay too. But is there any rhyme or reason to it?
In this article, we will attempt to sketch the outlines of a model for valuing graded cards.
Today, we will attempt to show that (for base cards at least) the Expected Value of a graded card should eventually approach the cost of the raw card plus the cost of grading.
But let us begin with a thought experiment which will illustrate why there is generally a downward pricing pressure on graded cards pushing the crack towards the marginal cost of grading.
One Grade World
To understand what drives the crack between graded cards and raw cards, let’s start by imagining a world (World A) in which three things are true:
There is only one grading company (GradeCo) and it has one service level for which it charges $50 including shipping and packaging supplies. In other words, it costs $50 total to get a card graded and there is no other option for grading.
The grading company only gives out one grade. If you send your card in (and it is authentic, which we assume the cards are) then it will receive a grade of “Graded” and get slabbed.
There are unlimited numbers of any card that people want to grade.
Now, we know that this is nothing like the real world, but bear with us.
So then, what will be the price of a Graded card in World A? In the long run, it will be about $50 more than the price of a raw card. Why?
Let’s say I am the first person in World A to submit Card X to GradeCo. Card X is worth about $100 raw. I pay $50 and a few weeks later I get my Card X back in a slab and now it is Graded (remember there is only one grade here in World A). Wooohooo! I have the first Graded Card X in all of World A. . . Pop 1 baby. So what do I do? Well I list it on eBay of course (World A has eBay). This listing is going to deserve at least three or four fire emojis in the title - so people know this is real fire.
Anyway, I list the card and it sells for $500 - a $350 profit. Not bad. But then what happens? We are assuming that people are at least predictable economic actors here so it’s not hard to guess. Everyone is going to start sending in their Card Xs to get that sweet Graded slab from GradeCo and make $350 of their own. And as we all know from Econ 101, when supply goes up, price goes down.
Indeed, people will keep submitting cards and driving down the price with an influx of Graded card supply until it doesn’t make sense to send cards in anymore - i.e., when the price of a Graded card is the same as the price of a raw card plus the cost of grading.
But obviously World A is nothing like reality. So let’s make it a little more realistic. . .
A World of Grades
Let’s travel now to World B. A world way more like earth. In World B, there is still only one grading company, but they have discovered grades! Good for them.
Now, when you submit Card X (a card from this year) to GradeCo, it will receive a number grade on a 1-10 scale (whole numbers only). So now what happens? Let’s say I submit my Card X and it gets a GC10 (GradeCo 10). “Amazing,” I think. I better get this thing listed up on eBay and sold. There are no comps because it’s the first one ever graded so I just list it as an auction and it sells for $800. Score! I made $650 ($800 - $100 (raw card) - $50 (cost of grading)).
But from our time in World A, we know what will happen next - if there is an easy $650 to be made, people will flood GradeCo with Card X submissions. Now though, when someone submits a Card X for grading, it might not get a GC10 - it could get a GC8, GC9, or if you are really unlucky a GC7 or lower.
In the weeks after I sell my GC10, hundreds of people will submit Card Xs to GradeCo and a couple things will happen. First, prices for GC8, GC9, and GC10 graded cards will start to settle. Second, the population report will begin to reveal how difficult it is to get each grade.
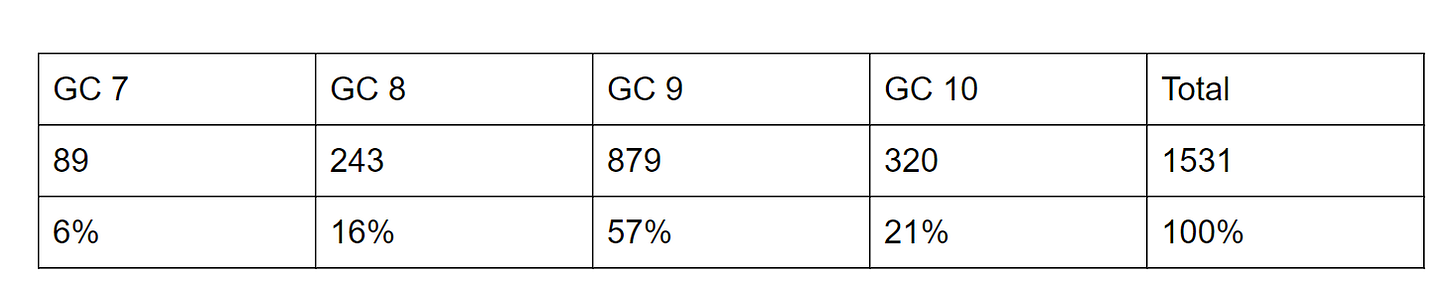
After some time, the population report for Card X in World B might look something like this:
And prices might look something like this (remember, a raw Card X costs $100):
This information allows us to calculate the expected return of submitting a Card X to GradeCo using some basic Expected Value math [NB: the math is the same regardless of how you acquire your raw Card X. Either you buy it for $100 or you pack it yourself in which case you could sell it for $100 but you don’t]:
As you can see, a few months after submissions of Card X began, it is “EV+” to submit your card. Of course, if you are really good at identifying which cards will grade well, then maybe you can eke out even better value. But the assumption we make here is that everyone thinks they are smarter than everyone else and so with modern base cards like Card X in our example, the actual grade you end up with is just weighted by the population totals.
In other words, no one submits a modern base card thinking that it will get an 8 - people submit cards that they think will grade well (which is why the grades tend to lean high). It just happens that sometimes people are wrong (not you though, other people).
So then, what does the $119.90 expected value tell us about Card X? It means that people will keep submitting cards, of course. And we know what happens then from our time in World A - prices of graded cards will drop.
[NB: We assume in both World A and World B that the price of the raw Card X remains constant. In other words, nothing is going on that would change the price of all Card Xs generally. Player X is not having a great year or getting hurt, Elon Musk is not crashing crypto prices, etc. . . This allows us to single out the effect on its price of grading a card without having to account for other factors.]
To summarize, in a world with one grading company and infinite cards, the expected return of submitting a card for grading will approach 0.
OK, so what does that mean for . . .
The Real World
Obviously, World B is a bit more like the real world than World A, but it is still only a poor facsimile.
Two obvious differences come to mind, only one of which we can sidestep for now. First, there are not unlimited cards - not even 1990 Topps. We have lots of things to discuss in the future regarding how rarity alone affects value. But for purposes of this article we want to focus on grading and therefore shift our focus just to graded base cards. For modern cards at least, base cards might not be unlimited, but they are plentiful enough that the rarity of a raw card will not materially impact price. In future articles, we will dive way deeper into the relationship between rarity and price and circle back to grading then too.
Second, unlike World B, there is not only one grading company here on earth. This has important ramifications. Indeed, the perceived “quality” of one grading company’s brand over another is one of the things that might keep expected returns elevated above 0.
Let’s take a look at a real world example that will allow us to explore this further as well as some other issues that arise.
A Zion Case Study
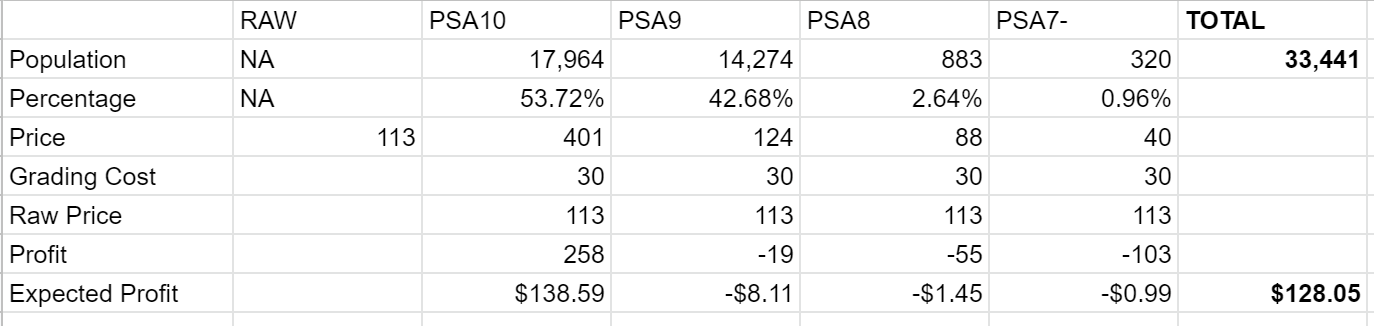
By looking at the PSA Population report and using data from Sports Card Investor’s Market Movers app, we can build a table like the ones we built above but for a real life card. Here, we have chosen Zion Williamson’s 2019 Prizm Base card. There was no sales data available on Market Movers for anything lower than a PSA 8 so we combed some eBay sales and found the sale of a PSA 7. We have used that price for anything below a PSA 8.
The other piece of data that we need is the submission cost to PSA. This is obviously impossible to know exactly because PSA has different service levels. But PSA knows and as we will soon see, this data should be important to them. For now, we assume that the average submission price is $30.
This allows us to create this chart:
This was not planned. But it looks like this 2019 Zion card is in a similar situation to our imaginary Card X in World B above. So what does this mean? Well, it’s a bit complicated because you can’t easily submit cards to PSA right now. But setting that aside, if this pricing table still looks like this when PSA reopens fully for submissions (and if it still costs about $30 to submit a card), it means that you if you buy a clean looking Zion 2019 Prizm Base off eBay and submit it to PSA you should make about $128 minus transaction costs.
Our theory suggests that this will put a general negative pricing pressure on PSA graded versions of that Zion card. Of course, it could also put upward pricing pressure on the raw versions of the card.
Despite those pressures, the $128 delta appears to have persisted. Why?
Well, maybe because we are just wrong idiots. But I don’t think so. Our theory is based on some pretty basic math and economics principles. It is not, however, complete. There are obviously other factors at play. So what might they be?
What Are We Missing?
Most obviously, it could just take a long time for the $128 delta to slowly approach zero. In the meantime, people can make money by going through the process of buying a raw card and taking the risk of getting it graded.
More likely, however, is that a large reason the delta exists is that it has to in order for people to submit cards. Basically, it is a payment to collectors who are willing to: 1) do the work of submitting a card; and 2) take the risk of submitting a card. But isn’t the risk factored into the calculation you ask? Yes and no. The risk of getting a bad grade is factored in, but not the risk that while the card is at PSA Zion gets injured or starts sucking.
In other words, if there wasn’t a $128 expected return from submitting the card then less people would submit the card, this would cause the supply to increase more slowly. The price would go down a little more and even fewer people would submit the card. Eventually (but before you got to $0) people just couldn’t be bothered. Submitting a card to PSA is not hard but it is a bit of a pain the ass. Part of the $128, then, is perhaps best viewed as the market’s compensation for going through the trouble and assuming the risk of PSA submissions.
Another factor that is not accounted for by our theory is that in the real world there is more than one card grading company. Because of this, consumer demand for the PSA brand might apply upward pricing pressure to the graded Zion cards in our example. In that regard, it is good news for PSA that the expected return on submitting cards to them is so large. This makes sense. After all, the expected return is basically a modified version of the crack adjusted for probable submission outcome and costs.
So What Does It All Mean?
Good question. There is a lot to chew on here with regard to card grading and pricing. But I think the three key points are:
1) In theory, the expected return of submitting a card for grading should approach 0.
2) In real life, it does not always do that because, among other possible reasons, people demand compensation for their effort and for bearing the risk of submission.
3) Generally, the further away from 0 the expected return is, the more “prestigious” the grading company.
This also raises several important questions that we don’t address here. What is the market price that collectors demand for submission? Is that the same across sports/eras? What happens if cards are not virtually unlimited? How does grading affect price for numbered parallel cards?
Perhaps most interestingly, however, the expected return can be the same with vastly different spreads between the graded prices. You can get to the same result if a graded 9 is worth half as much as a graded 10 or 1/20th as much as a graded 10. Here we focus on the price differences between raw cards and graded cards. But what about the price difference between cards with different grades. What causes that? Is it just a product of rarity?
Imagine there is a card numbered to 25 and all 25 cards are graded by PSA . If there are 20 PSA 10s and only 5 PSA 9s, does that mean that the PSA 9’s should actually be worth more than the 10? If not, why not? This will be the subject of a future article for sure.
This rarity issue bring us to one last thing to consider . . .
Graded Cards in our Valuation Framework
Before we go, our past few articles have focused on how to value cards. Astute readers might have noticed, however, that we did not really touch on grading in any of those articles. So how does grading fit into our valuation framework?
As I am quite certain you recall, our framework suggests that a card’s value is determined by a combination of three things: Quality, Rarity, and Market. You can read alllllll about that here. But basically:
Quality refers to how good the player on the card is - LeBron James is higher quality than Kevin Love.
Rarity is pretty self explanatory. A card numbered to 25 is rarer than a card numbered to 100. Base cards can be more rare than other base cards depending on print run.
Market is the most confusing but basically is a constant that accounts for the fact that, for instance, basketball cards are more valuable than hockey cards and quarterbacks are more valuable than defensive ends.
So how does grading a card fit into our framework? There is really only two ways that it could. Grading a card won’t change the quality of the player.
But, as mentioned above, grading creates rarity. Perhaps grading best fits into the framework as part of rarity then. There might be more to it than that though. Instead (or in part), graded cards might just be in a separate market for purposes of our framework. In other words, a PSA 10 might be more valuable because it is more rare but also because there is something about being a PSA 10 that is just more valuable.
We will try to tease that out in future articles. But I think we have given you enough to think about (or ignore) for now.
Until next time . . . .